Logistic Regression: Demystifying Classification with the Sigmoid Function

Logistic regression is a fundamental and widely used statistical and machine learning technique for classification problems. Unlike linear regression, which predicts continuous outcomes, logistic regression predicts the probability that an instance belongs to a particular class. It's a powerful and interpretable method, particularly well-suited for binary classification (two classes), but it can also be extended to multi-class problems. This article delves into the workings of logistic regression, focusing on the crucial role of the sigmoid function, its relationship to probabilities, and practical implementation in Python.
1. From Linear Regression to Logistic Regression
Linear regression, while powerful for predicting continuous values, isn't suitable for classification. Trying to directly predict a class label (e.g., 0 or 1) with linear regression has several problems:
- Unbounded Predictions: Linear regression can produce predicted values outside the range of 0 and 1, which doesn't make sense for probabilities.
- Violation of Assumptions: The assumptions of linear regression (linearity, normality of errors, homoscedasticity) are typically violated when the dependent variable is categorical.
Logistic regression solves these issues by introducing a crucial transformation: the sigmoid function.
2. The Sigmoid Function (Logistic Function)
The sigmoid function, also known as the logistic function, is the heart of logistic regression. It's an S-shaped curve that takes any real-valued number and maps it to a value between 0 and 1. This is exactly what we need for probabilities.
- σ(z) represents the sigmoid function's output (a probability between 0 and 1).
- z is a linear combination of the input features and their coefficients (similar to the input in linear regression).
- e is the base of the natural logarithm (approximately 2.71828).
- Interpretation: The sigmoid function transforms the linear combination of input features (z) into a probability. This probability represents the likelihood that the instance belongs to the positive class (usually labeled as 1).
Graphical Representation:

As z approaches positive infinity, σ(z) approaches 1. As z approaches negative infinity, σ(z) approaches 0. When z is 0, σ(z) is 0.5.
Equation:
\[ \sigma(z) = \frac{1}{1 + e^{-z}} \]
Where:
\(σ(z)\) is the output probability (between 0 and 1).
(z) is the input (the linear combination of features: \(b_0 + b_1x_1 + b_2x_2 + ... + b_nx_n)\).
\(e\) is the base of the natural logarithm (approximately 2.71828).
3. The Logistic Regression Model
The logistic regression model combines the linear combination of features with the sigmoid function:
P(Y = 1 | X) = σ(β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ)
= 1 / (1 + e⁻⁽β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ⁾)
Where:
- P(Y = 1 | X): The probability that the dependent variable Y belongs to class 1, given the input features X.
- X₁, X₂, ..., Xₚ: The independent variables (features).
- β₀: The intercept.
- β₁, β₂, ..., βₚ: The coefficients (weights) for each feature. These coefficients are learned from the training data.
- σ(z): The sigmoid function.
Key Differences from Linear Regression:
- Output: Logistic regression predicts a probability (between 0 and 1), while linear regression predicts a continuous value.
- Link Function: Logistic regression uses the sigmoid function as a link function to connect the linear combination of features to the probability.
- Loss Function: Logistic regression uses a different loss function called log loss (or cross-entropy loss), which is suitable for probabilities. Linear regression typically uses Mean Squared Error (MSE).
- Assumptions: Logistic regression has its own set of assumptions.
4. Log Loss (Cross-Entropy Loss)
The goal of training a logistic regression model is to find the coefficients (β₀, β₁, ..., βₚ) that minimize the log loss (also called cross-entropy loss). Log loss penalizes the model more heavily for confident incorrect predictions.
- y is the true class label (0 or 1).
- p is the predicted probability of the positive class (output of the sigmoid function).
- Interpretation:
- If y = 1 (true class is positive) and p is close to 1 (model is confident and correct), the loss is close to 0.
- If y = 1 and p is close to 0 (model is confident and incorrect), the loss is very high (approaches infinity).
- If y = 0 (true class is negative) and p is close to 0 (model is confident and correct), the loss is close to 0.
- If y = 0 and p is close to 1 (model is confident and incorrect), the loss is very high.
Equation (for the entire dataset):
Loss = - (1/n) * Σ [yᵢ * log(pᵢ) + (1 - yᵢ) * log(1 - pᵢ)]
Where: n is the number of instances. yᵢ is the true class for the i-th observation. pᵢ is the predicted probability for the i-th observation.
Equation (for a single instance):
Loss = - [y * log(p) + (1 - y) * log(1 - p)]
Where:
The model's parameters are typically found using optimization algorithms like gradient descent to minimize the log loss.
5. Interpreting Coefficients
The coefficients in logistic regression have a slightly different interpretation than in linear regression. They represent the change in the log-odds of the outcome for a one-unit increase in the predictor variable, holding all other predictors constant.
- Log-Odds: The log-odds is the logarithm of the odds ratio. The odds ratio is the ratio of the probability of an event occurring to the probability of it not occurring:
odds = p / (1 - p). So,log-odds = log(p / (1 - p)). - Exponentiating Coefficients: To get a more intuitive interpretation, we often exponentiate the coefficients (calculate
e^β). This gives us the odds ratio.e^β > 1: A one-unit increase in the predictor is associated with an increase in the odds of the positive class.e^β = 1: The predictor has no effect on the odds.e^β < 1: A one-unit increase in the predictor is associated with a decrease in the odds of the positive class.
Example: If the coefficient for "study hours" is 0.5, then e^0.5 ≈ 1.65. This means that for every additional hour of study, the odds of passing the exam (positive class) increase by a factor of 1.65, holding other factors constant.
6. Assumptions of Logistic Regression
While logistic regression is more robust than linear regression for classification, it still has assumptions:
- Binary Outcome (for binary logistic regression): The dependent variable must be binary (two categories). For multi-class problems, use multinomial logistic regression or one-vs-all strategies.
- Independence of Observations: Observations should be independent of each other.
- Linearity in the Logit: The relationship between the log-odds of the outcome and the independent variables should be linear. This is not the same as a linear relationship between the probability and the independent variables.
- No Perfect Multicollinearity: Independent variables should not be perfectly correlated with each other.
- Large Sample Size: Logistic regression performs better with large sample sizes.
- Low Multicollinearity: Like Linear Regression, avoid strong correlation between the independent variables.
7. Python Code Example (using Scikit-learn and Statsmodels)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report, roc_auc_score, roc_curve
import statsmodels.api as sm
# --- Generate Sample Data (Binary Classification) ---
np.random.seed(42)
n_samples = 200
X = np.random.rand(n_samples, 2)
# Create a linear relationship in the log-odds
y = (1 + 2 * X[:, 0] - 3 * X[:, 1] + np.random.randn(n_samples) * 0.5) > 0
y = y.astype(int) # Convert to 0 and 1
# --- Create a Pandas DataFrame (optional) ---
df = pd.DataFrame(X, columns=['X1', 'X2'])
df['y'] = y
# --- Split Data into Training and Testing Sets ---
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# --- Scikit-learn Logistic Regression ---
model_sklearn = LogisticRegression()
model_sklearn.fit(X_train, y_train)
# Make predictions
y_pred_sklearn = model_sklearn.predict(X_test)
y_prob_sklearn = model_sklearn.predict_proba(X_test)[:, 1] # Probabilities for the positive class
# Evaluate the model (Scikit-learn)
print("Scikit-learn Model:")
print(" Accuracy:", accuracy_score(y_test, y_pred_sklearn))
print(" Confusion Matrix:\n", confusion_matrix(y_test, y_pred_sklearn))
print(" Classification Report:\n", classification_report(y_test, y_pred_sklearn))
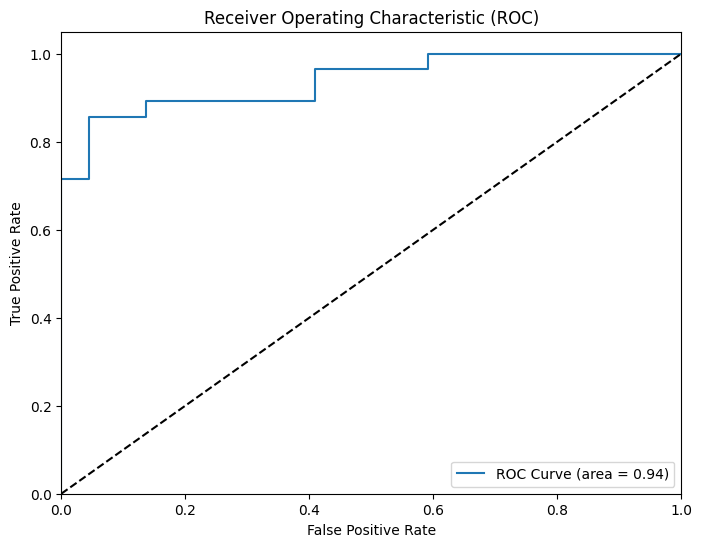
print(" ROC AUC:", roc_auc_score(y_test, y_prob_sklearn))
# ROC Curve
fpr, tpr, thresholds = roc_curve(y_test, y_prob_sklearn)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, label='ROC Curve (area = %0.2f)' % roc_auc_score(y_test, y_prob_sklearn))
plt.plot([0, 1], [0, 1], 'k--') # Random guessing line
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc="lower right")
plt.show()
# --- Statsmodels Logistic Regression (for more detailed statistics) ---
X_train_sm = sm.add_constant(X_train) # Add a constant (intercept)
model_statsmodels = sm.Logit(y_train, X_train_sm)
results = model_statsmodels.fit()
# Print model summary
print("\nStatsmodels Model Summary:")
print(results.summary())
# Get odds ratios
print("\nOdds Ratios:")
print(np.exp(results.params))
Output of the code:
Scikit-learn Model:
Accuracy: 0.8
Confusion Matrix:
[[13 9]
[ 1 27]]
Classification Report:
precision recall f1-score support
0 0.93 0.59 0.72 22
1 0.75 0.96 0.84 28
accuracy 0.80 50
macro avg 0.84 0.78 0.78 50
weighted avg 0.83 0.80 0.79 50
ROC AUC: 0.9383116883116883
Optimization terminated successfully.
Current function value: 0.265952
Iterations 8
Statsmodels Model Summary:
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 150
Model: Logit Df Residuals: 147
Method: MLE Df Model: 2
Date: Wed, 12 Feb 2025 Pseudo R-squ.: 0.5561
Time: 08:44:42 Log-Likelihood: -39.893
converged: True LL-Null: -89.871
Covariance Type: nonrobust LLR p-value: 1.971e-22
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 4.5279 1.093 4.143 0.000 2.386 6.670
x1 6.5692 1.436 4.575 0.000 3.755 9.384
x2 -11.4073 2.223 -5.132 0.000 -15.764 -7.051
==============================================================================
Odds Ratios:
[9.25598789e+01 7.12822643e+02 1.11140895e-05]
Key Code Explanations:
- Imports: Similar to linear regression, we import necessary libraries.
- Data Generation: Creates a synthetic dataset for binary classification.
- Train/Test Split: Splits the data.
- Scikit-learn Model:
LogisticRegression(): Creates a logistic regression model object.fit(): Trains the model.predict(): Predicts class labels (0 or 1).predict_proba(): Predicts probabilities for each class. We take[:, 1]to get the probability of the positive class (class 1).- Evaluation metrics:
accuracy_score,confusion_matrix,classification_report,roc_auc_score,roc_curve.
- Statsmodels Model:
sm.add_constant(): Adds the intercept.sm.Logit(): Creates a Logit model (logistic regression).fit(): Fits the model.results.summary(): Provides a detailed statistical summary, including coefficients, standard errors, p-values, confidence intervals, and goodness-of-fit statistics.np.exp(results.params): Calculates the odds ratios by exponentiating the coefficients.
- Advantages and Limitations of Logistic Regression
Advantages:
- Simplicity and Interpretability: Logistic regression is easy to understand and implement. The coefficients have a clear interpretation: they represent the change in the log-odds of the outcome for a one-unit change in the corresponding predictor variable.
- Efficiency: It's computationally efficient, especially for datasets with a relatively small number of features.
- Probability Outputs: It directly provides probability estimates, which are valuable in many applications.
- Regularization: L1 and L2 regularization can be used to prevent overfitting, especially when dealing with high-dimensional data.
- Online Learning: It can be easily updated with new data using techniques like stochastic gradient descent, making it suitable for online learning scenarios.
- Baseline Model: It serves as a good baseline model for comparison with more complex algorithms.
Limitations:
- Linearity Assumption: It assumes a linear relationship between the features and the log-odds of the outcome. This may not hold for all datasets, and performance may be poor if the relationship is highly non-linear.
- Multicollinearity: Performance can degrade if there's high correlation between the features.
- Outliers: Sensitive to outliers.
- Imbalanced Data: Can perform poorly on imbalanced datasets (where one class has significantly fewer instances than the other). Techniques like oversampling, undersampling, or using class weights can help mitigate this.
- Not Suitable for Complex Relationships: For very complex relationships between features and the outcome, more powerful algorithms (like decision trees, random forests, or neural networks) may be more appropriate.
- Practical Tips for Tuning and Evaluation
- Hyperparameter Tuning:
C(Regularization Strength): The inverse of regularization strength. Smaller values ofCspecify stronger regularization (which can help prevent overfitting). Use cross-validation (e.g.,GridSearchCVorRandomizedSearchCVin scikit-learn) to find the optimal value ofC.penalty: Specifies the type of regularization: 'l1' (LASSO), 'l2' (Ridge), or 'elasticnet' (combination of L1 and L2).solver: Choose the optimization algorithm based on dataset size and the type of penalty.class_weight: Can be set to 'balanced' to automatically adjust weights inversely proportional to class frequencies in the input data, which is helpful for imbalanced datasets.
- Evaluation:
- Accuracy: A simple metric, but can be misleading for imbalanced datasets.
- Precision and Recall: Precision measures the proportion of true positives among the predicted positives. Recall measures the proportion of true positives among the actual positives.
- F1-Score: The harmonic mean of precision and recall.
- ROC AUC: Area Under the Receiver Operating Characteristic Curve. A good metric for evaluating the overall performance of a binary classifier, especially for imbalanced datasets. It plots the true positive rate against the false positive rate at various threshold settings.
- Cross-Validation: Use k-fold cross-validation (e.g.,
cross_val_scorein scikit-learn) to get a more robust estimate of the model's performance.
- Feature Scaling: It's often beneficial to scale the features (e.g., using
StandardScalerorMinMaxScalerin scikit-learn) before training a logistic regression model, especially if the features have different ranges. This can help the optimization algorithm converge faster and improve performance. - Feature Engineering: Creating new features from existing ones can sometimes improve model performance. For example, you could create interaction terms (multiplying two features together) or polynomial features.
- Handling Imbalanced Data: As mentioned earlier, techniques like oversampling, undersampling, or adjusting class weights can be very important.
10. Conclusion
Logistic regression is a powerful and interpretable classification algorithm that leverages the sigmoid function to predict probabilities. Understanding the sigmoid function, log loss, and the interpretation of coefficients is crucial for effectively using and interpreting logistic regression models. The Python code examples, using both Scikit-learn and Statsmodels, provide a practical foundation for applying logistic regression to your own classification problems. Remember to check the assumptions of the model and choose appropriate evaluation metrics based on your specific problem and goals.
References
(1) Articles and Tutorials:
- Scikit-learn Documentation: Logistic Regression
- StatQuest: Logistic Regression (YouTube)- Excellent visual explanation.
- Logistic Regression (Machine Learning Mastery)
- An Introduction to Statistical Learning (ISLR)- Chapter 4 covers logistic regression in detail.
(2) Information on the Sigmoid Function:
(3) Python Code Examples:
(4) Academic References and Research Papers:
[1] Hosmer, D. W., Lemeshow, S., & Sturdivant, R. X. (2013). Applied logistic regression (3rd ed.). John Wiley & Sons.
[2] Agresti, A. (2013). Categorical data analysis (3rd ed.). John Wiley & Sons.
[3] James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: with Applications in R. Springer.
[4] Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.
[5] Kleinbaum, D. G., Kupper, L. L., Nizam, A., & Rosenberg, E. S. (2013). Applied regression analysis and other multivariable methods. Cengage Learning.


Comments ()