Convolutional Neural Networks (CNNs): A Comprehensive Guide

Image generated by Dall-E

Motivation

Traditional machine learning models struggle to directly handle raw image data due to the high dimensionality and complex spatial structure of images. A color image of modest resolution (say 200×200 pixels with 3 color channels) has 120,000 input features if flattened into a vector. Fully connected neural networks (multilayer perceptrons) that treat each pixel as an independent feature would require an enormous number of parameters and would ignore the spatial locality of pixel patterns. For example, a one-megapixel image fed into a single fully connected layer of 1000 neurons would demand on the order of 10^9 weights – an impractical number that would be extremely hard to train without massive data and computation. Clearly, a naive densely connected approach is inefficient for images and prone to overfitting.

Images have important local structures: nearby pixels are usually correlated and form meaningful features (like edges, corners, textures) that are spatially localized. Traditional ML approaches often required manual feature extraction (e.g., detecting edges or corners using algorithms like Sobel filters or SIFT) before classification. Fully connected networks lack a built-in mechanism to exploit spatial locality – they treat a pixel in the top-left of an image as unrelated to one in the bottom-right, unless the model learns it from data, which is inefficient. In contrast, convolutional neural networks (CNNs) embed the prior knowledge that local patterns matter: they use sparse connectivity and weight sharing across spatial locations to drastically reduce the number of parameters and focus on local feature extraction. In a CNN, each neuron in the first convolutional layer looks at only a small patch of the image (e.g., a 5×5 region) rather than the entire image, and the same set of filter weights is used for every such patch. This means the network learns one set of local patterns (a filter) and applies it across the whole image, detecting that pattern wherever it appears. This property greatly improves efficiency and translational invariance – a pattern detected in one location can also be recognized in another location of the image.

Another key motivation for CNNs is hierarchical learning. Visual data has hierarchical structure: simple patterns (edges, blobs) combine to form mid-level features (corners, textures), which combine to form high-level features (object parts), and so on. CNNs naturally support this hierarchy by stacking multiple layers of convolutions and pooling. The early layers of a CNN learn to detect low-level features like edges; later layers build upon those to detect higher-level shapes and objects. This mirrors how the human visual cortex has multiple stages of feature detection. Traditional flat models cannot easily learn such hierarchical representations. By extracting local features and composing them hierarchically, CNNs achieve far better performance on image tasks than models lacking this structure.

In summary, CNNs address the shortcomings of traditional approaches by introducing locality, weight sharing, and hierarchy. Compared to fully connected networks, CNNs require far fewer parameters (mitigating overfitting) and are more robust to shifts and distortions in the input (thanks to local receptive fields and pooling). These characteristics make CNNs especially powerful for computer vision tasks, which is why CNNs have become the de facto approach for image recognition, object detection, and many other vision problems.

How CNNs Work

A CNN is composed of a sequence of layers that transform an input image volume into an output (e.g. class probabilities) through a differentiable function. The high-level architecture of a typical CNN consists of: (1) one or more convolutional layers that act as learnable feature extractors, (2) activation functions (like ReLU) introducing non-linearity, (3) optionally pooling layers that downsample feature maps, and (4) fully connected layers at the end that perform high-level reasoning and output the final predictions. Modern CNNs often stack multiple conv and activation layers, occasionally interspersed with pooling, to progressively build a rich feature hierarchy.

Convolutional layers: In a conv layer, neurons are organized in feature maps (channels) and each neuron is connected only to a small region of the previous layer’s output – this region is called the neuron’s receptive field. A set of learnable weights (called a filter or kernel) is applied over this local region to compute a linear activation. The same filter (i.e., the same weight values) is slid across the entire input spatially, producing a feature map which is the map of responses of that filter at each position. Each filter detects a particular pattern (feature) in the input, and if that pattern appears anywhere in the image, the filter will produce a strong activation at the corresponding spatial location. Multiple different filters (hundreds in modern CNNs) operate in parallel in a conv layer, so the layer produces as many feature maps as there are filters. Stacking these feature maps along the depth dimension yields the output volume of the conv layer. Because of weight sharing, the number of parameters in a conv layer is just (filter_height × filter_width × input_channels) per filter, instead of per image location – a dramatic reduction compared to full connectivity.

After the linear convolution operation, CNNs apply a non-linear activation function to each element of the feature maps. The most common choice is the Rectified Linear Unit (ReLU), which is simply f(x) = max(0, x). ReLU sets negative values to zero, introducing non-linearity without affecting the receptive fields. ReLU is popular because it avoids saturation (which mitigates vanishing gradients) and is cheap to compute. In fact, the rectified linear activation has become the default for modern CNNs. Other activations like sigmoid or tanh were used in early networks but are now less common in deep CNNs due to slower convergence. In practice, applying ReLU after each convolution helps the network learn complex patterns and increases the nonlinear representational power.

Pooling layers: Periodically, a CNN will include a pooling (subsampling) layer to reduce the spatial resolution of feature maps and aggregate information. A pooling layer operates on each feature map independently and summarizes local regions into a single value (thus reducing width and height, but not depth). The most typical is max pooling, which takes the maximum value in each region (e.g. 2×2 window) and discards the rest. For example, a 2×2 max pool with stride 2 will shrink a 28×28 feature map to 14×14, by taking the max of each non-overlapping 2×2 block. Another option is average pooling, which takes the average of the region. Pooling provides three main benefits: (1) it reduces computation and parameters in later layers by shrinking feature map size, (2) it introduces a degree of translational invariance – small shifts or distortions in the input have less effect after pooling, since the maximum or average in a region is relatively stable, and (3) it can help combat overfitting by compressing information. In essence, after a convolution extracts features, pooling distills the strongest signals (in the case of max pooling) or an overall summary (average pooling), while reducing data size. Pooling is usually applied after some convolution layers. However, it is not mandatory after every conv layer; design choices vary, and sometimes strided convolutions are used in place of pooling for downsampling.

After several convolutional and pooling layers, a CNN’s final output is a set of high-level feature maps. For image classification, it is common to then use one or more fully connected (FC) layers to interpret these features and produce the final classification. The feature maps are typically “flattened” into a single vector, which is fed into one or more dense layers just like a standard neural network. Each fully connected layer takes all inputs from the previous layer (no spatial structure now, since we’re at the end) and computes an output. The last fully connected layer often has as many outputs as there are classes, and is followed by a softmax activation to produce class probabilities. (For regression tasks, it might output a single value or multiple values without softmax.) The role of the convolutional and pooling part of the network (often called the “conv base” or feature extractor) is to transform the image into a form that the fully connected layers can use for classification. In modern architectures, sometimes the final pooling is replaced by a global average pooling that directly computes one average for each feature map, avoiding the need for a flatten operation, but the principle is similar.

CNN architecture design choices: There are several considerations when designing a CNN architecture. One is the number of convolutional layers and their filter sizes. Early CNNs like LeNet-5 used 5×5 filters; later networks like AlexNet and VGG found success with multiple smaller filters (3×3) stacked sequentially, which can achieve the effect of a larger receptive field with fewer parameters and added non-linearities. The number of filters (depth of feature maps) typically increases in deeper layers, since we expect higher-level features to be more numerous or complex – for example, a first conv layer might learn 32 filters (detecting basic edges or colors), while a last conv layer may have 256 or 512 filters detecting various object parts. Another choice is how often and where to apply pooling. A common pattern is to increase the number of filters after pooling reduces spatial size, to preserve information capacity. Other design elements include the use of padding (usually “same” padding to maintain spatial size after conv, or “valid” padding to not pad), and the use of stride (a stride > 1 can downsample directly by skipping positions). Modern CNNs also incorporate normalization layers (e.g., Batch Normalization) and regularization techniques (Dropout) between layers to stabilize training, though these are not unique to CNNs. Overall, the architecture is usually structured so that early layers (few filters, high resolution) capture low-level features, and later layers (many filters, low resolution) capture high-level semantics, with a gradual transition controlled by pooling or strides. Figure 1 shows an example of a typical CNN flow from an input image through convolutions, pooling, and fully connected stages.

Mathematical Foundations

At its core, a convolutional layer performs a convolution operation on the input image or feature map. In the context of CNNs, we typically deal with discrete 2D convolutions. Mathematically, a discrete convolution of an input function $x(i,j)$ with a filter (kernel) $w(a,b)$ can be written as an output feature map $y(i,j)$ given by:

where $K_h \times K_w$ is the filter size (e.g., 3×3). This formula assumes we are doing a valid convolution (no padding) and the filter is being applied in a standard way (actually this formula is for cross-correlation – see note below). Each output $y(i,j)$ is the dot product of the filter weights $w(a,b)$ with a corresponding $K_h \times K_w$ patch of the input $x$ positioned at $(i,j)$. In a CNN, the input $x(i,j)$ would be the pixel values (or values in a feature map from the previous layer), and $y(i,j)$ is the filtered output. If the input has multiple channels $C_{\text{in}}$ (e.g. RGB image has 3 channels), the filter $w$ will have the same depth and the sum is taken over all channels:

where $w_c(a,b)$ are the filter weights for channel $c$ and $b$ is a bias term. Here $y(i,j)$ would be one output feature map (one filter’s response). A conv layer usually has $C_{\text{out}}$ such filters, each producing its own output map; so the full output of the conv layer is $C_{\text{out}}$ feature maps, which we can denote $y_k(i,j)$ for $k = 1,\dots,C_{\text{out}}$.

Padding and output size: Without padding, a $K_h \times K_w$ filter can only be applied where it fully fits on the input. For an input of size $H \times W$, a valid convolution (no padding) will produce an output of size $(H - K_h + 1) \times (W - K_w + 1)$ (assuming stride 1). Often we want to preserve the input size or control the output size, which is why zero-padding is used. Padding the input with $P$ pixels of zeros on each side increases the effective input size, allowing more positions for the filter. With padding $P$ and stride $S$ (stride is the step by which the filter moves each time), the output spatial dimensions $H_{\text{out}} \times W_{\text{out}}$ are given by the formula:

For example, if $H=W=28$ (as in MNIST images), $K=5$, $P=2$ (same padding), and $S=1$, then $H_{\text{out}} = (28 - 5 + 4)/1 + 1 = 28$, so the output remains 28×28. If stride $S>1$, the filter jumps in larger steps, yielding a smaller output. For instance, $S=2$ roughly halves the output size (with some difference if the input size isn’t perfectly divisible). Figure 2 illustrates three padding cases: no padding (shrinks output), zero-padding to keep size, and more exotic padding modes. In practice, “same” padding (output size = input size) is often used when we want to stack many conv layers without shrinking, whereas “valid” (no padding) is used when we explicitly want the feature maps to get smaller, or at the network edges.

Stride controls how the convolution filter moves across the input. A stride $S$ means we shift the filter by $S$ pixels between adjacent applications. Stride in effect downsamples the output: with $S=2$, we only compute every other position, halving the output resolution. Larger stride reduces computational cost but can miss some detail because we skip positions. Usually, stride 1 is used for most conv layers (to not miss any detail), and pooling layers or specific conv layers are responsible for downsampling. But strided convolution (e.g., $S=2$) can replace pooling – many modern architectures do strided convs to reduce size while learning (the strided filter can also learn which information to preserve). One must ensure the stride divides the input size appropriately (or use padding) so that the filter “tiles” the input evenly.

Dilation: In some CNN variants, dilated convolutions (also known as atrous convolutions) are used. Dilated convolution introduces a spacing between filter weights, effectively “inflating” the kernel by inserting zeros between its elements. A dilation rate $d$ means we sample the input at intervals of $d$: e.g., with $d=2$, we convolve using input values that are 2 pixels apart, treating one pixel in between as a gap. This increases the receptive field without increasing the filter size or number of parameters. For example, a 3×3 filter with dilation 2 covers a 5×5 area of the input (as if the kernel had holes between elements). Dilation is useful in tasks like segmentation or dense prediction, where we want a larger receptive field to incorporate more context without losing resolution via pooling. Mathematically, a dilated convolution of rate $d$ can be written as:

By adjusting $d$, we can make the conv layer look at every pixel ($d=1$, standard convolution), every second pixel ($d=2$), etc. Note that when $d>1$, some positions are skipped (holes), so usually one uses dilation in later layers when feature maps are small but need broader context.

The computational complexity of a convolutional layer depends on the filter size, number of filters, input size, etc. If the input is of size $H\times W$ with $C_{\text{in}}$ channels, and we have $C_{\text{out}}$ filters of size $K_h \times K_w$, and assume stride 1 for simplicity, then each output feature map has roughly $H_{\text{out}} \times W_{\text{out}}$ elements (where $H_{\text{out}} \approx H$ if padding is used). Each output element involves a sum of $C_{\text{in}} \times K_h \times K_w$ multiplications. Thus, the total number of multiply-add operations for the conv layer is on the order of $H_{\text{out}} \times W_{\text{out}} \times C_{\text{in}} \times C_{\text{out}} \times K_h \times K_w$. For example, a conv layer with input 64×64×3, 16 filters of size 5×5, and stride 1 would perform $64 \times 64 \times 3 \times 16 \times 5 \times 5 \approx 7.8$ million operations. This is much less than a fully connected layer connecting a similar-sized input to 16 neurons (which would be $64643*16 \approx 1.97$ million weights but with each output just a single number – not directly comparable without considering output size). In CNNs, convolution dominates the computation, but these operations are highly parallelizable (matrix-multiply-like operations on GPUs). It’s also worth noting that many algorithms and libraries optimize convolution, e.g. using FFT or lowering to matrix multiplication (im2col), and exploit sparsity or smaller bit-widths to speed up execution.

Despite the large number of operations, CNNs are feasible to train on modern hardware, and design choices like small kernels (3×3) and sparsity make them efficient. Weight sharing means the number of learnable parameters in a conv layer is just $C_{\text{out}} \times C_{\text{in}} \times K_h \times K_w$ (plus $C_{\text{out}}$ biases). This is often significantly smaller than the number of connections. For instance, the 5×5 conv layer above has $16 \times 3 \times 5 \times 5 = 1200$ weights – tiny compared to millions of connections it computes over the image. This efficiency allows CNNs to train with relatively limited data and avoid extreme overfitting, while still being expressive enough to learn complex image features.

Note: Deep learning libraries typically implement convolution as cross-correlation (the filter is applied without flipping it), since the weights are learned anyway. In pure math terms, convolution involves flipping the filter kernel, but in CNNs we usually don’t flip (or we treat the filters as symmetric for learning purposes). This detail doesn’t affect learning – it just means the learned filter is mirrored relative to a mathematical convolution kernel. Practitioners use the term "convolution" for this operation in CNNs, as it’s conceptually similar and yields the same type of result.

Graphical Illustrations

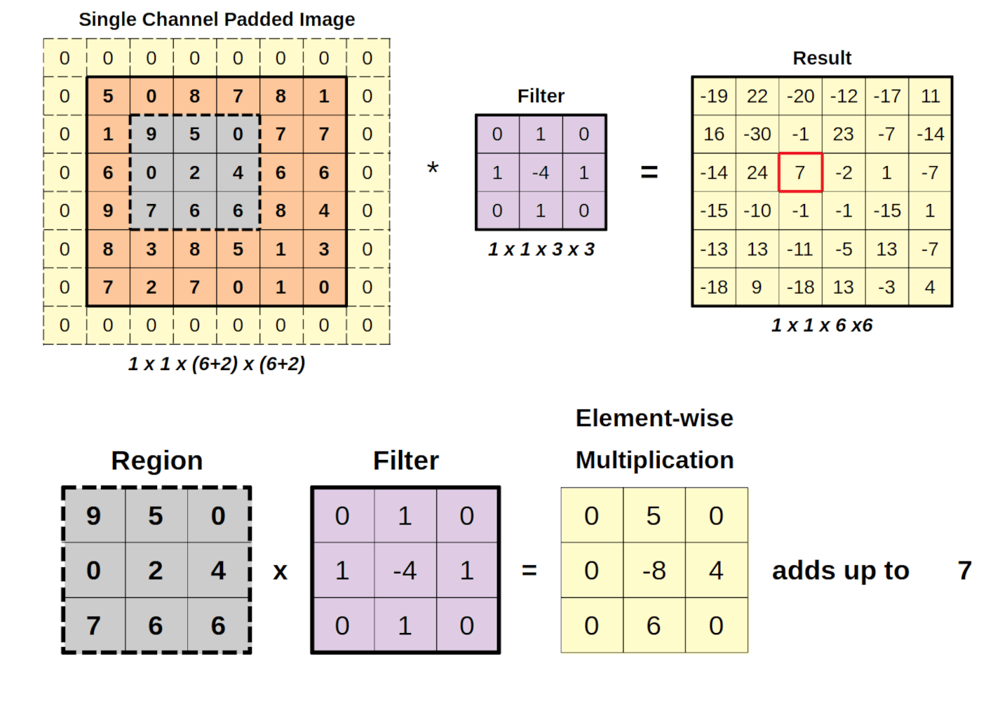
Figure 1: A worked example of a 2D convolution operation. The left shows a single-channel input image (orange numbers) that has been zero-padded with a 1-pixel border (light yellow)【18†】. A $3\times3$ filter (purple matrix) is applied to a local region (the gray-highlighted $3\times3$ patch) of the input. The element-wise multiplication between the filter and the input patch is shown at bottom (purple filter values times gray input values), and these products sum up to a single output value. In this example the sum is 7 (as highlighted in the red outline in the output matrix on the right). The filter then slides to the next position and the process repeats for each location. The result (right, yellow matrix) is the feature map produced by this filter, of size $6\times6$ in this case (since a $3\times3$ filter on a $8\times8$ padded input produces $6\times6$ output). This diagram illustrates how convolution computes each output pixel as a weighted sum of a local neighborhood of input pixels. Because the same filter weights are used at every location, the filter will produce high outputs wherever the pattern “matches” the input. Different filters would produce different feature maps (stacked depthwise in the conv layer output). This spatial weight sharing is key to CNNs’ efficiency and translation invariance.

Figure 2: Illustration of max pooling on a feature map. On the left is a $4\times4$ feature map (with distinct colors for quadrants). We apply a $2\times2$ max pooling with stride 2. This divides the input into four non-overlapping $2\times2$ regions (highlighted by colors). For each region, the maximum value is taken. For example, in the top-left (blue) quadrant, the values are {2, 2, 9, 4} and the maximum is 9; in the top-right (green) quadrant, max is 7; bottom-left (yellow) max is 8; bottom-right (red) max is 6. The output (right) is a $2\times2$ pooled feature map containing these maxima【24†】. Notice that the output has reduced spatial dimensions (from 4×4 to 2×2), capturing the strongest response in each region. This downsampling makes the representation more compact and provides a degree of translational invariance – e.g., if an important feature slightly shifts within that $2\times2$ window, the max pooled value still captures its presence. Pooling thus retains important features while discarding exact spatial details.

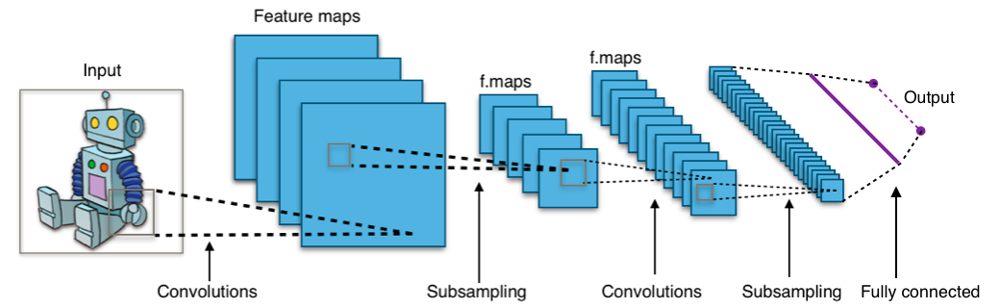
Figure 3: A typical CNN architecture for image classification. The input image (left, e.g. a robot cartoon) is first processed by convolutional layers, resulting in multiple feature maps (the stacked blue volumes) that represent detected low-level features. Each convolution is followed by a non-linearity (not shown) and often a subsampling (pooling) step (labeled as “Subsampling” in the diagram) that reduces spatial size【16†】. As we go deeper (to the right), the number of feature maps often increases (the blue stacks get thicker but spatial size gets smaller), indicating more complex features captured with less spatial resolution. After several conv and pooling stages, the final feature maps are flattened into a vector (illustrated by the series of blue squares being lined up) and passed through one or more fully connected layers (purple connections) to produce an output (such as class scores). The dotted lines indicate the flow of data: convolution preserves spatial structure (hence the feature maps aligned with specific parts of the input), while pooling gradually shrinks the width/height. This layered structure enables hierarchical feature learning: early layers detect edges and textures, intermediate layers detect parts of objects, and the final layers encode high-level representations leading to a decision about the image’s class.

Python Implementation using PyTorch

To solidify understanding, we will implement a simple CNN for image classification using PyTorch. In this example, we’ll use the MNIST dataset (handwritten digit images, 28×28 grayscale) for a basic demonstration. The steps include data loading, defining the model, training the model, and evaluating its performance. (PyTorch is a popular deep learning library with a flexible Python interface that makes building and training neural nets straightforward.)

Dataset: MNIST consists of 60,000 training images and 10,000 test images of digits 0-9. Each image is 1×28×28 (single channel). Our task is to classify each image into the correct digit class.

Below is a step-by-step guide with code snippets:

Data Preparation: We first load the MNIST dataset and prepare data loaders for training and testing. PyTorch’s torchvision.datasets provides a convenient way to download and use MNIST. We also normalize the image pixel values to the range [0,1] (or even mean-zero, but here 0-1 is fine since they are grayscale).


import torch
import torchvision
import torchvision.transforms as transforms

# Define a transform to normalize the data
transform = transforms.Compose([
    transforms.ToTensor(),  # convert images to PyTorch tensors
    # (optional) transforms.Normalize((0.5,), (0.5,))  # normalize to mean 0.5, std 0.5 if needed
])

# Download and load the training and test sets
train_dataset = torchvision.datasets.MNIST(root='./data', train=True,
                                           download=True, transform=transform)
test_dataset = torchvision.datasets.MNIST(root='./data', train=False,
                                          download=True, transform=transform)

train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1000, shuffle=False)

In this code, train_loader will iterate over the training dataset in mini-batches of 64 images, and test_loader provides batches of 1000 test images. We set shuffle=True for training so that each epoch sees data in a random order. We use torchvision.transforms.ToTensor() to convert the PIL images to tensors of shape [channels, height, width] with pixel values in [0,1]. (Normalization is commented out above; it can help training convergence but is not strictly necessary for this simple case.)

Model Definition: Next, we define our CNN model by subclassing torch.nn.Module. Our simple CNN will have two convolutional layers (with ReLU activations) and two pooling layers, followed by two fully connected layers. Specifically:

conv1: 1 input channel (grayscale) -> 16 output channels (filters), kernel size 3×3, padding=1
conv2: 16 input -> 32 output channels, kernel size 3×3, padding=1
Each conv is followed by ReLU and a 2×2 max pooling (stride 2).
After two conv+pool layers, the feature map size is reduced from 28×28 to 7×7 (since 28 -> 14 -> 7 with two pools).
We then flatten and use a fully connected layer fc1 (3277 inputs -> 128 hidden units) with ReLU, and a final fc2 (128 -> 10 outputs for the 10 classes).

import torch.nn as nn
import torch.nn.functional as F

class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, stride=1, padding=1)
        self.conv2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, stride=1, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)  # 2x2 pooling
        self.fc1 = nn.Linear(32 * 7 * 7, 128)   # 32 feature maps of size 7x7 -> 128 hidden units
        self.fc2 = nn.Linear(128, 10)          # 10 output classes

    def forward(self, x):
        # Convolution -> ReLU -> Pool (layer 1)
        x = self.conv1(x)
        x = F.relu(x)
        x = self.pool(x)
        # Convolution -> ReLU -> Pool (layer 2)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.pool(x)
        # Flatten feature maps into a single vector per image
        x = x.view(x.size(0), -1)  # same as reshape to (batch_size, 32*7*7)
        # Fully connected layer -> ReLU
        x = self.fc1(x)
        x = F.relu(x)
        # Output layer (no activation here, we will apply softmax via loss)
        x = self.fc2(x)
        return x

model = SimpleCNN()
print(model)

When we print the model, we see its architecture. The model’s forward pass applies each layer in sequence. We use F.relu from torch.nn.functional for the activation function. Note that we did not explicitly include a softmax layer at the end; in PyTorch, it’s common to apply softmax as part of the loss (e.g., CrossEntropyLoss expects raw logits and applies softmax internally). The model has learnable parameters (weights and biases) in conv1, conv2, fc1, fc2. Thanks to weight sharing, conv1 has $11633 = 144$ weights + 16 biases, conv2 has $163233 = 4608$ weights + 32 biases, fc1 has $(3277)128 \approx 200k$ weights + 128 biases, and fc2 has $12810 = 1280$ weights + 10 biases. This is around 206k parameters in total – quite manageable for training.

Training the CNN: Now we train the model on the MNIST training data. We define a loss function and an optimizer. For multi-class classification, cross-entropy loss is appropriate. We’ll use PyTorch’s nn.CrossEntropyLoss, which combines a softmax and log-loss. As optimizer, we can use stochastic gradient descent (SGD) or Adam. Here we use SGD with a learning rate of 0.01 for simplicity.

import torch.optim as optim

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# Training loop
num_epochs = 3
for epoch in range(num_epochs):
    model.train()  # set model to training mode
    running_loss = 0.0
    for images, labels in train_loader:
        # Forward pass: compute predictions
        outputs = model(images)
        loss = criterion(outputs, labels)
        # Backward pass and optimization
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    # Print average loss for this epoch
    avg_loss = running_loss / len(train_loader)
    print(f"Epoch {epoch+1}/{num_epochs}, Training loss: {avg_loss:.3f}")

In each epoch, we loop over the training dataset in batches. For each batch:indicating the loss dropped as the model learned. (These numbers are illustrative; actual values may vary slightly.)

outputs = model(images) does a forward pass, producing a 10-dimensional score for each image (corresponding to classes 0-9).
We compute the loss against the true labels. criterion(outputs, labels) expects labels as the ground-truth digit indices (0-9).
We zero the gradients, call loss.backward() to compute gradients for all parameters, and then optimizer.step() to update the weights. We also accumulate the loss to monitor training progress. We run a few epochs (e.g., 3). On MNIST, even 1-2 epochs with this simple model will already yield good accuracy (as MNIST is relatively easy). We print the average loss per epoch to see it decreasing. For instance, you might see output like:

Epoch 1/3, Training loss: 0.300
Epoch 2/3, Training loss: 0.100
Epoch 3/3, Training loss: 0.080

Evaluation: After training, we evaluate the CNN on the test dataset to see how well it generalizes to unseen data. We measure the classification accuracy.

model.eval()  # set model to evaluation mode
correct = 0
total = 0
with torch.no_grad():  # no need to compute gradients for evaluation
    for images, labels in test_loader:
        outputs = model(images)
        # outputs are of shape (batch_size, 10); the predicted class is the index of max score
        _, predicted = torch.max(outputs, 1)  # get the index of the max logit
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
accuracy = 100 * correct / total
print(f"Test Accuracy: {accuracy:.2f}%")

Here we disable gradient computation (since we’re only doing forward passes). We loop through the test data, get the model’s predictions, and use torch.max to find the class with highest score for each image. We compare against the true labels to count correct predictions. Finally, we compute the percentage of correct predictions. A well-trained simple CNN on MNIST can achieve ~98-99% test accuracy. Even with just 3 epochs as above, you might see accuracy around 97%+.

This implementation demonstrates a basic CNN and how to train it. For a more complex dataset like CIFAR-10 (color images of size 32×32), the same principles apply but the network might need to be deeper or have more filters, and training takes longer. PyTorch makes it easy to experiment with different architectures – you could add more convolutional layers, change kernel sizes, or use a different optimizer (like Adam) with just a few lines of code changes.

Sources & References

Zhang, Aston, et al. Dive into Deep Learning, Chapter 7: Convolutional Neural Networks (2020) – An open-source deep learning textbook that provides an overview of CNN concepts and examples.
Wikipedia: Convolutional neural network – Comprehensive article on CNNs, including history and technical details.
Alzubaidi, Laith, et al. “Review of deep learning: concepts, CNN architectures, challenges, applications, future directions.” Journal of Big Data, vol. 8, no. 1, 2021, Article 53. (A thorough review of CNN developments; cited for sparse connectivity and weight sharing explanations).
PapersWithCode: Dilated Convolution Explained – Online description of dilated (atrous) convolutions with definitions.
GeeksforGeeks: “CNN – Introduction to Pooling Layer” – Tutorial explaining pooling layers; source of the max pooling illustration.
Goodfellow, Ian, et al. Deep Learning. MIT Press, 2016 – See Chapter 9 (Convolutional Networks) for a deep dive into the mathematical and theoretical aspects of CNNs.
PyTorch Documentation: Training a classifier – Official tutorial on training a CNN for image classification (similar to the code used in this article).
Krizhevsky, Alex, et al. "ImageNet classification with deep convolutional neural networks." Communications of the ACM, vol. 60, no. 6, 2017, pp. 84-90. (Originally NeurIPS 2012) – A landmark paper (AlexNet) demonstrating the power of CNNs on the ImageNet image recognition challenge, spurring the deep learning revolution in computer vision.